En general, se puede decir que un fractal es un objeto irregular con patrones que se repiten a diferentes escalas. Sin embargo, no es un concepto matemático formal, sino que engloba varios conceptos sobre objetos geométricos, funciones, etc.
Un ejemplo de fractal típico es el conjunto autosimilar, que es un objeto que está compuesto por copias más pequeñas de sí mismo, como el triángulo de Sierpinski:

Otros ejemplos típicos surgen al estudiar las órbitas de funciones definidas en los números complejos, como los conjuntos de Julia y el conjunto de Mandelbrot:



En la Universidad de Almería podíamos encontrar una construcción de la tercera iteración del fractal conocido como «esponja de Menger», coordinada por el profesor José Luis Rodríguez. Su construcción resulta de dividir un cubo en otros 27 cubos, eliminando los que ocupan las posiciones centrales. Esta construcción forma parte del proyecto MegaMenger, en el que se han realizado 20 terceras iteraciones en universidades, museos e institutos de todo el mundo. La esponja de Menger es un objeto fractal con dimensión mayor que 2, pero menor que 3. A continuación se puede ver una imagen del resultado de la construcción de este fractal.

No hay muchas herramientas para estudiar objetos fractales. Una de las más importantes es la dimensión fractal. La dimensión de un punto es 0, la de una curva suave es 1, y la de una superficie suave es 2. Sin embargo, la dimensión fractal del triángulo de Sierpinski, por ejemplo, es 1,5849… lo que nos sindica que está a medio camino entre una curva y una superficie. Esta dimensión, por tanto, es una medida de la complejidad del objeto, y puede servir para diferenciar entre distintos objetos. Es por esto por lo que se aplica en numerosos campos donde los fractales aparecen de forma natural, como la medicina, la ecología, las finanzas, la biología, la geología, etc.
Fractales en nuestro jardín
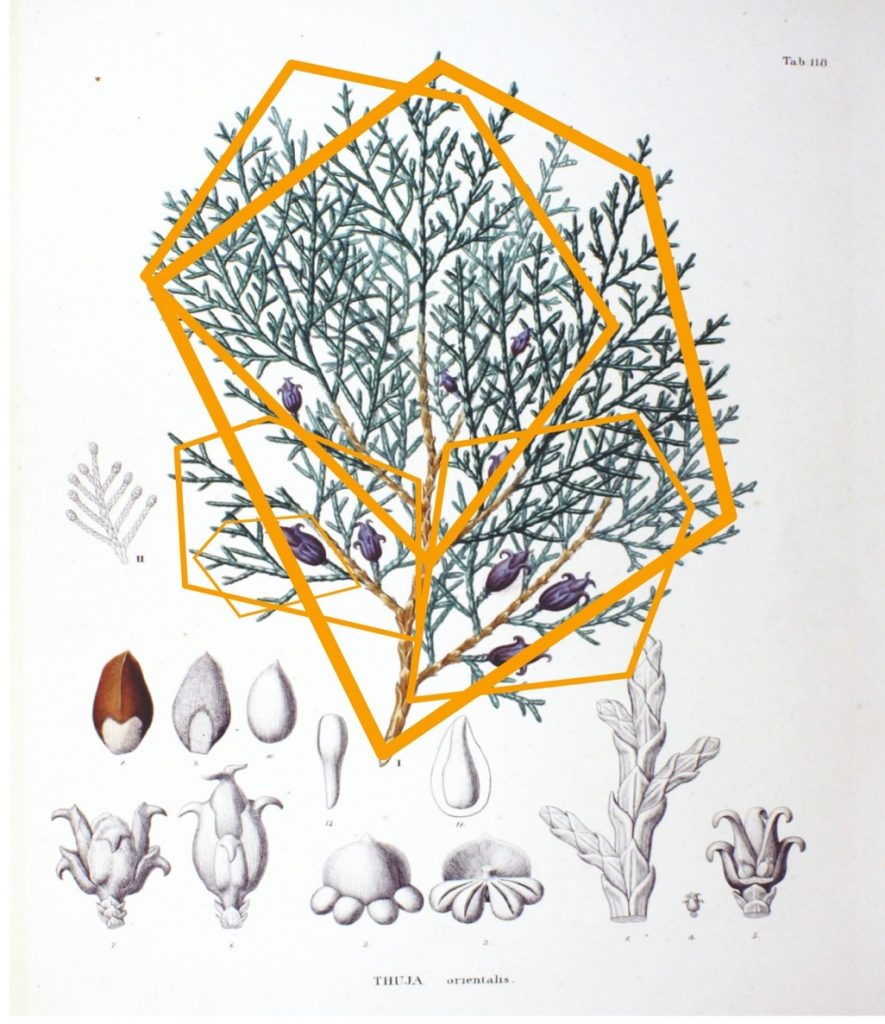
El Platycladus orientalis es un árbol de hoja perenne y nativo de China. En la siguiente imagen podemos observar su propiedad de autosemejanza. Se puede observar cómo la estructura de la planta se replica a distintas escalas en los recuadros señalados en color naranja.
Experimenta los fractales
Con lo aprendido, ahora puedes ponerte a prueba con las siguientes actividades.
Actividad 1
Haz una foto de una planta del jardín que te parezca fractal y encuentra el patrón que se repite a escalas más pequeñas.
Introducción a las actividades 2 y 3
Los conjuntos autosimilares en el plano se pueden generar a partir de un conjunto de similaridades (también llamadas semejanzas) de la forma
f(x,y)=(a+(r \cos \ \theta )x-(r \ sen \ \theta )y, b+(r \ sen \ \theta)x+(r\ cos \ \theta )y)
con a y b reales, 0 \leq \theta \leq 2 \pi es el ángulo del giro y 0<r<1 es el factor de contracción
Un caso sencillo es cuando no hay giro ( \theta=0 ), con lo que la similaridad quedaría de la siguiente forma f(x,y)=(a+rx,b+ry) .
Por ejemplo, el triángulo de Sierpinski se genera con las tres similaridades
f_1(x,y)=(\frac{x}{2},\frac{y}{2})
f_2(x,y)=(\frac{x+1}{2}, \frac{y}{2})
f_3(x,y)=(\frac14 +\frac{x}{2}, \frac{y+1}{2})
En este caso el factor de contracción de las tres similaridades es \frac{1}{2} .
El Teorema de Moran nos dice cómo calcular la dimensión fractal de un conjunto autosimilar en función de los factores de contracción de las similaridades r_1, \ldots, r_n . La dimensión es la solución de la siguiente ecuación r_1^x+r_2^x+\ldots+r_n^x=1 .
Por ejemplo, para la triángulo de Sierpinski, la dimensión fractal se calcula como la solución de (\frac{1}{2})^x+(\frac{1}{2})^x+(\frac{1}{2})^x=1 , es decir, \frac{3}{2^x}=1 , con lo que 3=2^x . Si tomamos logaritmos, \log(3)=x \log(2) , donde hemos usado la propiedad \log(a^b)=b \log(a) . Por lo tanto, la dimensión fractal del triángulo de Sierpinski es \log(3)/\log(2) que es aproximadamente 1,585.
Actividad 2
Calcula la dimensión fractal del conjunto autosimilar alfombra de Sierpinski, que está generado por las similaridades:
f_1(x,y)=(\frac{x}{3},\frac{y}{3})
f_2(x,y)=f_1(x,y)+(\frac13,0)
f_3(x,y)=f_1(x,y)+(\frac23,0)
f_4(x,y)=f_1(x,y)+(0,\frac13)
f_5(x,y)=f_1(x,y)+(\frac23,\frac13)
f_6(x,y)=f_1(x,y)+(0,\frac23)
f_7(x,y)=f_1(x,y)+(\frac13,\frac23)
f_8(x,y)=f_1(x,y)+(\frac23,\frac23)
Solución: \frac{\log(8)}{\log(3)} .
Actividad 3
Calcula la dimensión fractal del conjunto autosimilar que está generado por las similaridades:
f_1(x,y)=(\frac{x}{2},\frac{y}{2})
f_2(x,y)=(\frac{x+1}{2}, \frac{y}{2})
f_3(x,y)=(\frac23 +\frac{x}{3}, \frac{y+1}{3})
Este conjunto autosimilar es una variación del triángulo de Sierpinski. Fíjate que en este caso no todas las similaridades tienen el mismo factor de contracción, con lo que la solución es más difícil de encontrar.
Solución: Aproximadamente 1,3646.