The last three times we were concerned with the Multiverse models each of those is highly connected with the notions of the Superstring theory. This time we are going to consider another model which rises from the notions of quantum mechanics with all its bizarreness. The idea was proposed by one of John Wheeler’s students Hugh Everett III, who came up with highly unexpected results trying to solve a long known problem of the Copenhagen interpretation to quantum theory developed by Niels Bohr and his team. It is surely quite a complicated task to provide all the relevant information on this topic in a short article, but I’ll try my best to encompass the most significant pieces of the story. For those who will like the idea and will want to dig in deeper I suggest the book “The Hidden Reality” written by Brian Greene a few years ago.

Let us start with a brief description of some concepts of quantum theory which we will need for the perception of the following idea. You might have noticed that physicists, speaking of various concepts, use the terms classical physics and quantum physics. Of these classical physics is referred to everything we had before quantum mechanics has taken its place. Newtonian dynamics, Maxwell’s electromagnetism, Einstein’s theories of relativity are all classical physics. But what makes quantum mechanics and later theories so different that we have separated them from classical ones? It has to do with the fact that all classical theories are completely deterministic. That is, if you have a system with a finite number of bodies (take for example our Solar system) and you know exactly their positions, velocities and several other factors, applying the laws of classical physics to this system you can get the exact information of their positions, velocities and so on in the future or in the past. And in this sense there is no limit to how far in the future or in the past we could get. This is what determinism is all about.

But quantum mechanics forced us to leave our hopes for the possibility that this could happen even in principle. Quantum mechanics is a theory of probabilities. This tells us that if you have the same initial data, applying the laws of quantum theory you can only get some value of probability that you will find your system, which is being analyzed, in some condition and another value of probability that you will find it in some other condition. Say, you are analyzing an electron that is placed in some box and you want to determine where you will find it a couple of seconds later. Applying the laws of quantum theory you can get, say, 55% likelihood that you will find the electron at the right top corner, 35% that you will find it at the left bottom corner and 10% that you will find it somewhere in between. In this sense, you have to complete many experiments to determine whether or not quantum theory’s predictions hold true. And this has been done to an unimaginable level of precision. Quantum mechanics has become the most precise theory we’ve ever had, its predictions match our experimental data so well that some physicists even suggested an analogy: the precision of quantum mechanics is the same as if you measure the distance between Los Angeles and New York and your mistake is equal to the width of human’s hair. The predictability of quantum theory isn’t applied to a particular experiment, but takes place only with a series of such experiments. If you perform 100 similar experiments with your electron, you will find it 55 times at the right top corner, 35 times at the left bottom corner and 10 times somewhere in between. Perform other 100 experiments and your results will be roughly the same. And this idea is applied not only to electrons, but to all the other elementary particles such as photons, quarks, neutrinos and such.

One of the main achievements of the physicists developed quantum theory was obtaining a mathematical formalism which could be consistent with this notion of probabilities. We have the main equation published by Erwin Schrödinger in 1926, which works perfectly and is still used by physicists. But what this equation does for us and why is it so useful? It determines the behavior of waves, and all the particles we aware of are also waves. To get the idea how this is possible we have to get some familiarity with the famous experiment of quantum mechanics which is called the double-slit experiment.

The idea of this experiment is the following: a coherent source of electrons (we are again assuming that our experiment deals with electrons but they can be replaced by any other elementary particles) emits them one by one in the direction of a plate pierced by two parallel slits. Electrons, passing through these slits, then observed on a screen behind the plate. Let’s assume we start our experiment with only one opened slit. In this case you will see your electrons only behind the opened slit. You can see it on the image below: when the top slit is opened, you get the electrons on the screen behind it, and if the top slit is closed and bottom one is opened, you see the electrons behind the bottom slit. Fair enough.

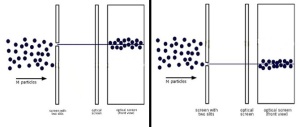
A decently reasonable reader who is not familiar with quantum mechanics’ concepts would expect a combined picture in the case with both slits being opened. However, if we open both of them something weird is happening.

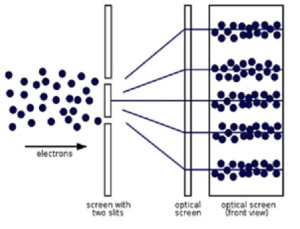
Instead of producing a combined picture, this experiment produces what is known in physics as the interference pattern (bright and dark bands on the screen shown above). Show this picture to a physicist and ask his first thought about it. He will immediately tell you: waves. Indeed, such interference pattern could only be produced by waves interacting with each other. If you have ever thrown a couple of heavy objects into water and observed the behavior of produced waves you have an idea of what I’m talking about. Where peaks of two waves meet, the resulting wave’s peak becomes higher; where a trough of one wave overlaps with a trough of the other, the resulting wave also has trough in that place; but when a peak of one wave coincides with a trough of another one, both waves cancel each other out. This is exactly what causes our picture to get this peculiar guise: an electron, being a particle, behaves as a wave at the same time, so when it comes to the plate it gets through both slits in a form of wave and then both waves interact with each other producing the bright bands where two peaks come together, less bright bands where the waves cancel each other partially and dark bands where two waves cancel each other completely.

Okay, this is all good, but what are these waves? And how could an electron, being a particle, behave like a wave at the same time?

The answer to this question suggested by a German physicist Max Born later brought him a Nobel Prize in physics. What Born suggested was that such a wave could be a probability wave. In our first experiment with an electron placed in a box we had the largest peak of the electron’s wave at the top right corner, a lesser peak in the left bottom corner and a small peak between the corners.

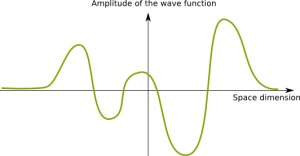
Accordingly, these peaks corresponded to the 55%, 35% and 10% probabilities of finding the electron in that place. The likelihood of finding it anywhere else is equal to zero. If you analyze behavior of a particle you should not think of it as of a solid thing traveling between two points. Instead, you should examine it as a wave propagating from one point to another. The result of double-slit experiment is explained by this concept. As we’ve seen, an electron comes to the plate, propagates through both slits and then two waves recombine and produce interference pattern on the screen.

The next question that might come to your mind is whether or not we could see or directly detect these probability waves. The answer to this question is actually unsatisfying: we cannot. According to the Copenhagen interpretation we have no chance to ever detect a probability wave, because when it is observed it instantly collapses everywhere leaving only one peak wherein we eventually detect our examined particle. This concept of collapsing wave functions is what led Hugh Everett to his proposal. The problem is that the behavior of those probability waves is perfectly described by Schrödinger’s equation, but according to the Copenhagen interpretation this equation is no longer applicable when the particle is observed by some macroscopic entity. In this case the entire wave collapses to a single peak and such a collapse can’t be modeled with Schrödinger’s equation for some mathematical reasons which we need not be concerned with here. So, said Bohr, we can use Schrödinger’s equation only until we observe the examined particle but we have to move it away at the moment of measuring. I know, such an awkward method of solving a problem sounds unscientific, but Bohr’s ability of convincing based on unassailable reasoning along with the phenomenal success of his model’s predictive power caused physical society to accept the Copenhagen interpretation. But Everett didn’t want to abandon Schrödinger’s equation even in the case of measuring. He used some rigorous mathematical constructions and came up with a really unexpected result.

As Brian Greene described it in his book, suppose we are performing an experiment injecting our electron into the mini-model of Paris. You have exact information about electron’s wave function at the start of the experiment. Analyzing the wave function you conclude that it has a 100% chance to be found somewhere around the Eiffel tower at a particular moment (we are assuming it has only one peak for the sake of simplification). And indeed, if you carry out this experiment you detect the electron around the Eiffel tower. The equipment in your laboratory determines its location and gives you information that it has been detected near the Eiffel tower.

Suppose now we have a slightly more complicated wave function with two peaks, one of those being still located near the Eiffel tower and the other one near the Arc de Triomphe. Analyzing it you conclude that your electron has a 50% likelihood of being found near the Eiffel tower and, consequently, 50% near the Arc de Triomphe. You perform your experiment and receive the information on your monitor that the electron has been found near the Eiffel tower. Another try and you detect it near the Arc de Triomphe. Carrying out 100 experiments you find that the first location has been identified nearly 50 times, and so is the second one.

If we were able to somehow see the wave function, our monitor should have shown us both locations –the Eiffel tower and the Arc de Triomphe – as a result of one measurement, which would signalize that the electron is located in two different places at the same time. This would seem confusing but still comprehensible. Now suppose we have a real wave function with thousands of peaks. In this case you would see all of these results on your monitor. This would end up with a headache and lead us to a complete bewilderment. Since a wave function can’t collapse according to Schrödinger’s equation, this is what we would always experience. But Bohr would say: take an anaesthetize, you will never see such a thing since the wave function collapses as soon as it’s been measured. And this standpoint is still a dominating one. But let’s now look at what Everett suggested.

The main problem that he and some other physicists saw in Copenhagen interpretation is that there is no reasonable explanation as to why Schrödinger’s equation can’t be applicable to the act of measurement, and the question which is more important, how can we rigorously distinguish between objects of micro-world and those of macro-world? For, albeit we, humans, are certainly objects of macro-world, we nevertheless consist of elementary particles which are micro-world objects. So why can’t Schrödinger’s equation be applicable for us or for any macro-object such as our detectors, laboratories and the like?

What Everett proposed is that it can be applicable, but in this case the question arises: if it is, why do we see only one outcome as a result of our experiment? Where do the others disappear? According to the Many-Worlds approach they all take place, all the peaks that correspond to an analyzed wave function appear each in a ‘new’ Universe. That is, in our experiment with a mini-model of Paris both configurations with the electron located near the Eiffel tower and the same one located near the Arc de Triomphe take place in two different Universes. While you measure the electron’s location and find it near the Eiffel tower, another Universe suddenly get born where an exact copy of you finds it near the Arc de Triomphe. If there are three possible outcomes, the third one appears for another copy of you in yet another Universe. As we have seen, sometimes a number of possible outcomes is really huge, and even in this case, each of them would take place in a distinct Universe. This may sound ironically, but the beauty of this approach is in its simplicity. Not the conceptual simplicity with a huge number of parallel Universes of course, but in mathematical simplicity. It is basically the most economical approach to quantum mechanics and the most elegant solution to the question as to why there remains only one outcome after a measurement out of all the possible outcomes.

You might wonder how all these other Universes “suddenly appear”. What is the mechanism which is capable of producing all of them? Do they somehow “split” from the initial one? This is where things get pretty bizarre. In this approach all of those Universes aren’t located somewhere in space like in all the other Multiverse models which we have covered so far. Here we have just different realities. Let me briefly explain how this can be the case. Mathematical framework of quantum theory is applied not only for a single particle and so is the Schrödinger’s equation. It can encapsulate all the other particles which include you and your laboratory, entire Earth, the Solar system, the Milky Way and even the entire Universe. In our experiment with the mini-model of Paris a particular peak corresponds not only to the likelihood of our electron to be detected near the Eiffel tower, but to such a configuration of all the particles in the entire Universe which forms a distinct reality where the electron is detected there. At the same time there is a similar configuration with the electron being located near the Arc de Triomphe. There is no mechanism which would literally split one Universe into two, instead they would be located, in a sense, at the same place but their realities would be slightly different. And the important thing about this model is that when I said “a copy of you finds it there”, you might have thought that it means that the Universe with your copy is somewhat less real than this one, where you find your electron near the Eiffel tower. But while this may seem pretty reasonable this is not how it works. All of those Universes are as real as this one!

The last thing that I should mention here might have already popped up in your head. If all the possible outcomes really take place, what does probability mean? If we say that the likelihood of our electron being found near the Eiffel tower is, say, 80% and near the Arc de Triomphe is 20%, what do we mean by these probabilities if both of them are realized in two different Universes? Doesn’t that mean that all the possible outcomes have 100% probability to take place? This is still highly debated question and many physicists reject the Many-Worlds interpretation because there is no definite answer to it. Everett himself suggested that probability appears in his approach as a consequence of the lack of data at the moment when we carry out an experiment. That is, if you toss a coin you know that the probability of the result is roughly 50% for both obverse and reverse sides of the coin. But if you knew the exact mass of your coin, its size, its momentum and a few other properties at the moment of tossing, you could calculate the result. But usually, our information is not sufficient and this is why we use probabilities.

Everett thought that something similar would be applicable for his approach. Suppose that mankind has developed a machine which is capable of cloning a human being. One day you find a letter in your mail where someone suggests you to participate in his experiment. He will clone you such that both you and a clone will in fact be yourself, but one of you will wake up tomorrow with $billion in his wallet while the other one will wake up as a slave in 500BCE with no chance of escaping and will remain a slave for the rest of his life. You won’t probably accept this since the stakes are too high. The next morning you find another letter where this person suggests that he will make a million clones, so the next morning one million of you will have a billion of dollars and only one will be a slave. Here you start to doubt since the likelihood of waking up being a slave is extremely tiny. Suppose you have accepted this and the author of the letter made a million of your clones, all of them being as real as you are. Or maybe even better would be to say that all of them are literally you. As soon as you start to wake up you recall what has happened and start to calculate in your mind the probability of becoming a slave. So do all of your copies. Eventually, one million of you find that they woke up being very rich and only one realized that the rest of his life will be a nightmare.

Everett suggested that this lack of information is the way for probability to appear in his approach. The inhabitants of one Universe have no information about what happens in others and they continue to subjectively rely on the concept of probability. In the Many-Worlds interpretation probability takes its place only as a subjective aspect, while the actual reality is purely deterministic and obeys the laws of physics and the Schrödinger’s equation in particular. However, Everett was not able to construct a mathematically consistent system for this statement that is why his approach is still highly debated among physicists.

I thank everybody for taking the time to read this article and see you next time.