The whole numbers, the first numbers we learn, are infinite. If you take a number and add one to it, you get a new and bigger number — but not always. Keep counting up from one and you can get to 213 — but start at one o’clock in the afternoon and you never get to two-hundred and thirteen o’clock. In this post we are going to look at a type of number where we cannot keep going forever. Instead, as we keep adding one, the numbers cycle around, like the numbers on a clock. It turns out that there is an infinite family of these number systems, and some of them obey almost all the normal rules of arithmetic.

When you are first learning to add and multiply, you might make tables. Memorizing the multiplication tables is somewhat controversial in math education (Occupy Math comes down firmly in favor of memorizing your one-digit multiplication facts). At the top of the post are addition and multiplication tables, but not the normal ones. This post is about a whole collection of number systems based on the integers, each of which has only a finite number of numbers. The addition and multiplication tables above have five numbers, for example. As we will see, these number systems show up in several applications. They obey many of the same laws of arithmetic as the integers. Mathematicians think of these number systems as smaller images of the integers that preserve some of their properties.

How do the integers (mod n) work?

Remember that if you divide two whole numbers you get a quotient and a remainder. If, for example, you take 14 and divide it by 4, then there are three 4s in 14 with 2 left over. One would say that fourteen divided by four is three with remainder two. Remainders are the key to the integers (mod n). You do the arithmetic the same way you would for the normal integers and then, when you are done, take the remainder you would get if you divided by n. You just throw away the quotient. The addition and multiplication tables at the top of the post are for the integers (mod 5). Let’s check one of the entries: 3×4=12 and 12 is two fives with remainder 2. We say that:

3×4=2 (mod 5)or “three times four equals two modulo five”.

The integers (mod n) exist for every positive n, but if n is a prime number, then the number system obeys more of the rules of arithmetic than when n is not prime. An example of a rule that the integers (mod n) do not obey is “start with 0 and keep adding 1 to a number and you get a new number every time”. This rule fails in the integers (mod n), but most of the other rules hold. One way to think of the integers (mod n) is that, when you count by ones, the numbers wrap back around to zero. If we count (mod 7), for example, the numbers go 0, 1, 2, 3, 4, 5, 6, 0, 1, 2, 3, 4, 5, 6, 0, 1, …

There is a rule that holds in the standard numbers, “if a×b=0, then a=0 or b=0“, that helps explain why the integers (mod n) are better behaved when n is a prime number. This rule still holds when n is prime, but it must fail if n is not prime. The number n has remainder zero when divided by n so n=0 (mod n). Keeping this in mind 2 × 2=4=0 (mod 4), showing that two numbers can multiply to make zero even when neither of those numbers is itself zero in the integers (mod n) when n is not prime.

There are some things to get used to. These new number systems have a whole different set of customs for what a negative number is. Learning different customs can be a job of work, but it expands your mind and imagination. This is like the way you mind expands when you travel to a foreign country. All the negative numbers (mod n) are also positive numbers (mod n). It may help to think about it this way. If m is a number, then negative m is the thing you add to m to get zero. For example, 2+3=5=0 (mod 5) which means that -2 is equal to 3 in the integers (mod 5), because you add 3 to 2 to get zero. Division is even weirder. Look at the multiplication table at the top of the post. For every number except zero, there is another number you can multiply that number by to get 1. For example, 2×3=1(mod 5). Since the thing you multiply 2 by to get 1 is 1/2 that means that, in the integers (mod 5), one half is equal to three. To divide by 2 in the integers (mod 5) you multiply by 1/2, which is 3. For example,

4÷2=4×1/2=4×3=12=2 (mod 5).

The integers (mod n) are very simple — but the way that the rules of arithmetic work out is fairly weird until you get used to it. One rule that makes things simpler is that when n, or a multiple of n, shows up in your arithmetic, then you can replace it with zero. In the rest of the post we will look at places the integers modulo n can be used.

Applications and examples

One way to tell computer scientists and mathematicians apart is that computer scientists tend to start counting things at zero, while mathematicians start counting things at one. These two ways of doing things have the nice, intuitive names zero-based counting and one-based counting. Zero based counting works much better in algorithms and when designing computer hardware — math being so much older, the math works on the basis that the first finger you hold up is finger number one. You can do zero based counting with your fingers, but holding up a fist to represent zero is not something everyone understands. It’s also potentially a little hostile, as a gesture. This discussion leads into our first example, clock arithmetic.

Two hours after eleven o’clock is not thirteen o’clock (it might be thirteen hundred hours if you are using military time). Two hours after eleven o’clock is one o’clock — and there we have the wrapping numbers. The integers (mod 12) count zero through eleven, but a clock counts one through twelve before starting over. Clocks use modular arithmetic, but a non-standard version of it where we shift everything over and use one-based counting. Nevertheless, this is an example of where the idea of wrapping numbers comes in.

The integers (mod 2) and logic

Logic is a mathematical system with two values, true and false. Instead of addition, multiplication, and negation, logic uses operations called “or”, “and”, and “not”. If a and b are logic values, then a or b is true if either a or b are true; a and b is true if both a and b are true; not a is true if a is false and it is false if a is true. It turns out that logic can be implemented with the integers (mod 2).

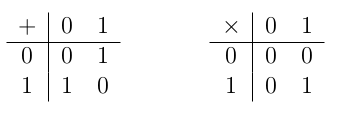
In the integers (mod 2) there are only two numbers: 0 and 1. Their addition and multiplication tables are shown above. If we make 0 represent false and 1 represent true, then

• a or b is the maximum of a or b,
• a and b is the minimum of a or b, and
• not a is 1-a.

So all the basic logic operations happen in the integers (mod 2). We are assuming that it is still true that 1 is bigger than 0 in the integers (mod 2) to do all this. We can use other arithmetic operations to obtain some other logic operations. There is a logic operation called exclusive or that is true if exactly one of its input values is true. Exclusive or is realized as addition (mod 2) — to see this, look at the addition table for (mod 2), given above.

What day of the week is December 14, 2025?

Occupy Math is writing this post on July 31, 2021, which is a Saturday. Google can tell you right away that Dec. 14, 2025 is 1,597 days away from “today”. The days of the week cycle just like the integers (mod 7): Sat, Sun, Mon, Tue, Wed, Thu, Fri, Sat, … If we assign Saturday to 0 (mod 7) and figure out which number (mod 7) that 1597 is, we can find the day of the week that Dec. 14, 2025 will be easily. You can do this by removing obvious multiples of seven, like this:
1597=1400+197
197=140+57
57=56+1
which means that 1597=1 (mod 7) and so Dec 14, 2025 is one day after Saturday in the week — it is a Sunday. Notice that 1400, 140, and 56=7×8 are all multiples of seven and, so, equal to zero (mod 7).

Using the internet to find out that Dec. 14, 2025 is 1597 days in the future from the day when Occupy Math is writing this post is the easy way to do it (and the internet can tell you the day of the week — use this to check Occupy Math’s result). As an in-class exercise, counting the number of days to a specific date can be interesting. You need the rules for leap years and the number of days in each month to do it correctly.

Latin Squares

A Latin square is an n-by-n array filled with n symbols so that each symbol appears exactly once in each row and each column of the table. Latin Squares appeared in the post Justice by Design: Latin Squares, and it turns out that the integers (mod n) give you a way of generating Latin squares. Latin squares can be used to avoid certain kinds of bias or unfairness when you are designing an experiment (read the other post for details) and so having a source of them is nice. Earlier in the post we show the addition tables for the integers (mod 5) and (mod 2) and you can see that (if we ignore the labels on the top and side) that these are Latin squares. We can go well beyond that, however. If a and b are not zero and n is prime, then filling a table with ax+by, where x is the position in the row (mod n) and y is the position in the column, (mod n) always gives us a Latin square. For an example, here is a table of 2x+3y (mod 7).

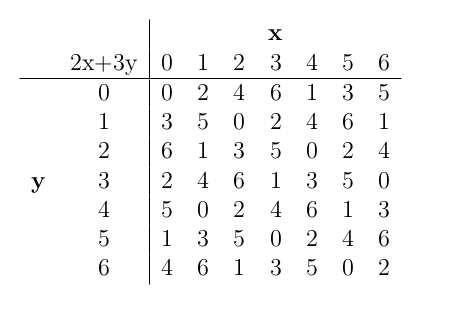
You may notice that the numbers in each row appear in the same order, just shifted over, and the same is true for the columns. This is the same effect of wrapping around you get when you count by ones (mod n), but you are counting by twos (in the rows) and by threes (in the columns). If n is not prime, then you can still make Latin squares this way, but you need a stronger rule than “a and b are not zero”. They have to be numbers that have no factors in common with n, except for one, which is always a common factor.

Solving hard problems with easy problems

Suppose that you wanted, in the integers (mod 3), to solve the equation 2x+1=0. To solve this problem, you would take one to the other side, divide by two, and get x=-1/2. In the integers (mod 3) there is another option: plug in zero, plug in one, and plug in two and see what works. Since 2×1+1=3=0 (mod 3) we see the answer is x=1 — which also means that 1=-1/2 (mod 3), more of that weird arithmetic. The point is this: solving an equation over the integers (mod n) can be done by plugging in every single number and seeing what works. Doing this with normal arithmetic is completely impossible — there are an infinite number of numbers — but in (mod n) it is sometimes the fastest method.

It turns out that we can use this to solve some really hard problems that use the normal sort of arithmetic. This is because, if an equation has a solution in the integers (mod n) and in the integers (mod m) then it also has a unique solution in the integers (mod m×n), as long as n and m have no common factors. Calculating this solution for a larger modulus uses a very old theorem discovered in China, called the Chinese Remainder Theorem, which Occupy Math covered in one of his fourth year classes. If the modulus is large enough — if we are doing the arithmetic (mod huge) — then the solution has the same value (mod huge) as it does in the normal numbers, and we have a solution that works back in the standard number system.

What makes this system practical is that we can solve the equation we are interested in — by trial plugging in — modulo many small primes and the product of those primes builds up really fast. If we solve an equation (mod 2), (mod 3), (mod 5), (mod 7), and (mod 11), then we can use the Chinese remainder theorem to get its solution (mod 2310), for example. This ability to solve hard problems by trial plugging in of numbers is one of the most powerful applications of the integers (mod n).

As you probably suspect, Occupy Math chose a few applications of the integers (mod n) out of a huge number that are out there in math. Other applications include encryption algorithms for secret codes, the creation of communications systems that still work in the presence of transmission noise, many problems in number theory, and many others. In addition, the integers (mod n) give us an infinite number of examples of number systems with a finite number of numbers, enriching the set of examples of number systems we have in mathematics.

I hope to see you here again,
So remember to get your Covid vaccination!
Daniel Ashlock,
University of Guelph
Department of Mathematics and Statistics