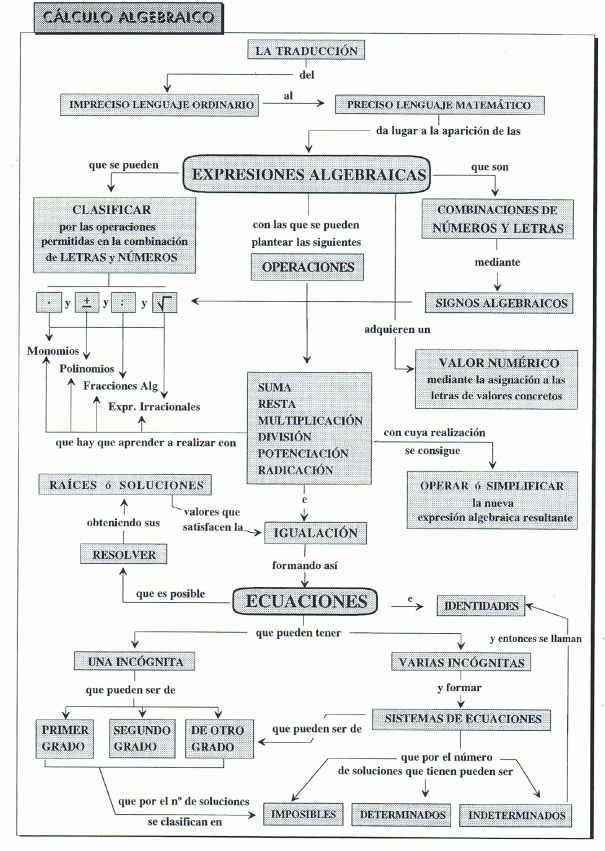
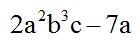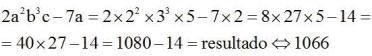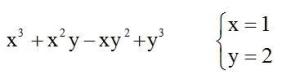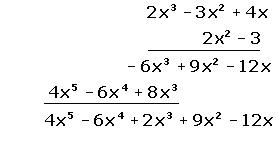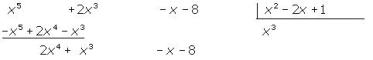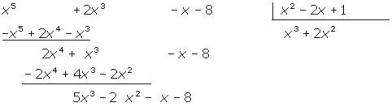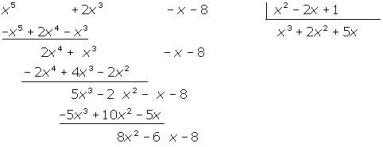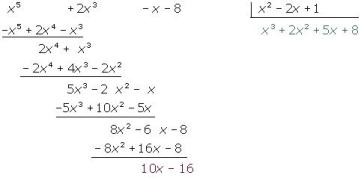¿Sé puede trabajar con CANTIDADES DESCONOCIDAS en matemáticas? Por ejemplo, no conozco tu edad, por eso la llamo x (de desconocida) Tampoco conozco la edad que tiene (o tendría) tu mamá, por eso la llamo y (cantidades DISTINTAS, letras DISTINTAS) Ya ves, en realidad no conozco nada. Y sin embargo, sé a ciencia cierta que y-x es la edad que tenía tu mamá cuando tu naciste. ¿No te parece magia? Sí, ésta es la MAGIA DE LAS MATEMÁTICAS. Sólo si tienes ALMA DE MAG@ te gustará el CÁLCULO ALGEBRAICO. Así:
Pero, ¿qué es el álgebra?
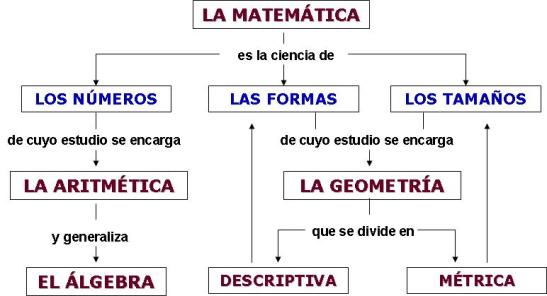
 EL ÁLGEBRA generaliza a la aritmética en el siguiente sentido. La aritmética estudia los números y sus operaciones en particular, ¡con números concretos!
EL ÁLGEBRA generaliza a la aritmética en el siguiente sentido. La aritmética estudia los números y sus operaciones en particular, ¡con números concretos! Esta rama se caracteriza por hacer implícitas las incógnitas dentro de la misma operación: LA ECUACIÓN ALGEBRAICA.
Esta rama se caracteriza por hacer implícitas las incógnitas dentro de la misma operación: LA ECUACIÓN ALGEBRAICA.Etimológicamente, proviene del árabe (también nombrado por los árabes Amucabala )??? (yebr) ( al-dejaber ), con el significado de reducción, operación de cirugía por la cual se reducen los huesos luxados o fraccionados (algebrista era el médico reparador de huesos).
Historia del álgebra
El álgebra tuvo sus primeros avances en las civilizaciones de Babilonia y Egipto, entre el cuarto y tercer milenio antes de Cristo. Estas civilizaciones usaban primordialmente el álgebra para resolver ecuaciones de primer y segundo grado.
 El álgebra continuó su constante progreso en la antigua Grecia. Los griegos usaban el álgebra para expresar ecuaciones y teoremas, un ejemplo es el teorema de pitagoras. Los matemáticos más destacados en este tiempo fueron Arquímedes, Herón y Diofanto. Arquímedes se basó en las matemáticas en su tratados de física y geometría del espacio. Herón fue otro que se basó en ellas para hacer algunos de sus inventos, como la primera máquina de vapor. Diofanto fue el griego que más contribuyó a esta área del conocimiento, como principales trabajos tenemos al análisis diofántico y la obra de Las Aritméticas, que recopila todo el conocimiento del álgebra hasta ese entonces.
El álgebra continuó su constante progreso en la antigua Grecia. Los griegos usaban el álgebra para expresar ecuaciones y teoremas, un ejemplo es el teorema de pitagoras. Los matemáticos más destacados en este tiempo fueron Arquímedes, Herón y Diofanto. Arquímedes se basó en las matemáticas en su tratados de física y geometría del espacio. Herón fue otro que se basó en ellas para hacer algunos de sus inventos, como la primera máquina de vapor. Diofanto fue el griego que más contribuyó a esta área del conocimiento, como principales trabajos tenemos al análisis diofántico y la obra de Las Aritméticas, que recopila todo el conocimiento del álgebra hasta ese entonces.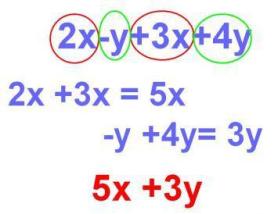 Como consecuencia, el álgebra cambió de rumbo y amplió su dominio a todas las teorías que se habían inventado alrededor del tema inicial, incorporando las teorías de los grupos matemáticos y sus extensiones, y parte de la geometría, la rama relacionada con los polinomios de segundo grado de dos variables, es decir las cónicas elipse, parábola, hipérbola, círculo, ahora incluidas en el álgebra bilineal.
Como consecuencia, el álgebra cambió de rumbo y amplió su dominio a todas las teorías que se habían inventado alrededor del tema inicial, incorporando las teorías de los grupos matemáticos y sus extensiones, y parte de la geometría, la rama relacionada con los polinomios de segundo grado de dos variables, es decir las cónicas elipse, parábola, hipérbola, círculo, ahora incluidas en el álgebra bilineal.El lenguaje Algebraico
- El lenguaje que usamos en operaciones aritméticas en las que sólo intervienen números se llama lenguaje numérico.
- El lenguaje que utiliza letras en combinación con números y signos, y, además, las trata como números en operaciones y propiedades, se llama lenguaje algebraico.
- La parte de las Matemáticas que estudia la relación entre números, letras y signos se llama Álgebra.
 El lenguaje algebraico nace en la civilización musulmana en el período de Al–khwarizmi, al cual se le considera el padre del álgebra. El lenguaje algebraico consta principalmente de las letras de alfabeto y algunos vocablos griegos. La principal función de lenguaje algebraico es estructurar un idioma que ayude a generalizar las diferentes operaciones que se desarrollan dentro de la aritmética, por ejemplo: si queremos sumar dos números cualesquiera basta con decir a + b; donde la letra a indique que es un número cualquiera de la numeración que conocemos, b de la misma manera que a significa un número cualquiera de la numeración.
El lenguaje algebraico nace en la civilización musulmana en el período de Al–khwarizmi, al cual se le considera el padre del álgebra. El lenguaje algebraico consta principalmente de las letras de alfabeto y algunos vocablos griegos. La principal función de lenguaje algebraico es estructurar un idioma que ayude a generalizar las diferentes operaciones que se desarrollan dentro de la aritmética, por ejemplo: si queremos sumar dos números cualesquiera basta con decir a + b; donde la letra a indique que es un número cualquiera de la numeración que conocemos, b de la misma manera que a significa un número cualquiera de la numeración.
Cómo aparecen las letras en matemáticas
Para trabajar con cantidades desconocidas y razonar de una manera precisa con ellas. Una cantidad desconocida se suele representar con alguna letra llamada variable. Ejemplos:
- Sea x mi edad.
- Sea y la edad de mi madre.
- Entonces y – x son los años que tenía mi madre cuando yo nací.
 Como vemos, empleamos letras para representar cualquier número desconocido, realizamos operaciones aritméticas con ellas e, incluso, las incluimos en expresiones matemáticas para poder calcular su valor numérico (ver ecuaciones).
Como vemos, empleamos letras para representar cualquier número desconocido, realizamos operaciones aritméticas con ellas e, incluso, las incluimos en expresiones matemáticas para poder calcular su valor numérico (ver ecuaciones).
Para poder manejar el lenguaje algebraico es necesario comprender lo siguiente:
- Se usan todas las letras del alfabeto.
- Las primeras letras del alfabeto se determinan por regla general como constantes, es decir, cualquier número o constante como el vocablo pi.
- Por lo regular las letras X, Y y Z se utilizan como las incógnitas o variables de la función o expresión algebraica.
 También el lenguaje algebraico ayuda mantener relaciones generales para razonamiento de problemas a los que se puede enfrentar cualquier ser humano en la vida cotidiana.
También el lenguaje algebraico ayuda mantener relaciones generales para razonamiento de problemas a los que se puede enfrentar cualquier ser humano en la vida cotidiana.
Aquí se presentan los siguientes ejemplos, son algunas de las situaciones más comunes que involucran los problemas de matemáticas con lenguaje algebraico; cualquier razonamiento extra o formulación de operaciones con este lenguaje se basa estrictamente en estas definiciones:
- un número cualquiera
Se puede denominar con cualquier letra del alfabeto, por ejemplo:
a = un número cualquiera
b = un número cualquiera
c = un número cualquiera
… y así sucesivamente con todos los datos del alfabeto.
- la suma de dos números cualesquiera
a+b = la suma de dos números cualesquiera
x+y = la suma de dos números cualesquiera
- la resta de dos números cualesquiera
a-b = la resta de dos números cualesquiera
m-n = la resta de dos números cualesquiera
- la suma de dos números cualesquiera menos otro número cualquiera
a-b+c =la suma de dos números cualesquiera menos otro número cualquiera
- el producto de dos números cualesquiera
ab = el producto de dos números cualesquiera
- el cociente de dos números cualesquiera (la división de dos números cualesquiera)
a/b= el cociente de dos números cualesquiera
- la semisuma de dos números cualesquiera
(a+b)/2= la semisuma de dos números cualesquiera
- el semiproducto de dos números cualesquiera
(ab)/2= el semiproducto de dos números cualesquiera
Características del lenguaje algebraico
- El lenguaje algebraico es más preciso que el lenguaje numérico: podemos expresar enunciados de una forma más breve.
El conjunto de los múltiplos de 5 es 5 • = {±5, ±10, ±15, …}.
En lenguaje algebraico se expresa 5 • n, con n un número entero.
- El lenguaje algebraico permite expresar relaciones y propiedades numéricas de carácter general.
La propiedad conmutativa del producto se expresa a • b = b • a, donde a y b son dos números cualesquiera.
- Con el lenguaje algebraico expresamos números desconocidos y realizamos operaciones aritméticas con ellos.
El doble de un número es seis se expresa 2 • x = 6.
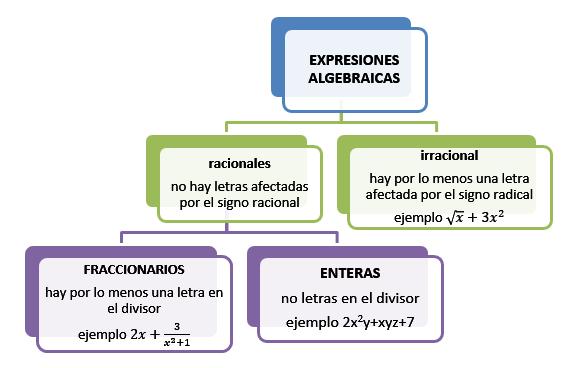
Expresiones algebraicas
 Una expresión algebraica es un conjunto de números y letras que se combinan con los signos de las operaciones aritméticas.
Una expresión algebraica es un conjunto de números y letras que se combinan con los signos de las operaciones aritméticas.
Las expresiones algebraicas surgen al traducir el impreciso lenguaje ordinario al preciso lenguaje matemático. A modo de ejemplos, ofrecemos un listado de frases con un contenido matemático traducidas al lenguaje algebraico:
- Teresa tiene x años: x
- Su hija tiene 25 años menos que ella: x -25
- Su madre tiene el doble de edad que ella: 2x
- Su padre le saca 6 años a su madre: 2x + 6
- Lorenzo tiene 5 años más que Teresa: x + 5
La INVISIBILIDAD en el álgebra
—A veces les digo a mis alumnos que tienen que utilizar unas gafas Matemáticas para usar en clase y que, les permitan ver «ciertas cosas» que sin ellas es imposible. Unas gafas de quitar y poner, ponérselas en clase y quitárselas cuando salgan, porque estar viendo Matemáticas todo el día puede trastornar a cualquiera. Aunque en determinadas ocasiones pueden, también, usarse fuera de clase, como por ejemplo: para el concurso de fotografía o para que no te engañen en la cuenta del hiper, …


Creo que para el próximo curso voy a encargar un par de centenares de esas gafas, ¿alguien sabe donde se venden?
Valor numérico de una expresión algebraica
 El valor numérico de una expresión algebraica es el número que resulta de sustituir las letras por números y realizar a continuación las operaciones que se indican. Se trata de una simple sustitución de letras por números para después hacer los cálculos indicados por la expresión y obtener así un resultado:
El valor numérico de una expresión algebraica es el número que resulta de sustituir las letras por números y realizar a continuación las operaciones que se indican. Se trata de una simple sustitución de letras por números para después hacer los cálculos indicados por la expresión y obtener así un resultado:
Ejemplo: Dada la expresión

Respuesta: 1066
Solución:
Sustituimos las letras por los números teniendo en cuenta los signos aritméticos:
Otro ejemplo: Calcula el valor numérico de 3a – 2b + 4a + 3b si a = 2 y b = 3
Respuesta: 17
Un más: Calcula el valor numérico de:
Respuesta: 7
Clasificación de las expresiones algebraicas
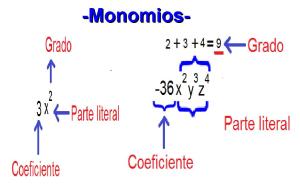
Monomios
Un monomio se define como aquella expresión algebraica que combina letra y números utilizando solo productos. Está constituida por coeficientes, exponentes y bases.
Coeficiente numérico: es la cantidad numérica o letra que se encuentra a la izquierda de la base, la cual indica la cantidad de veces que la base se debe sumar o restar dependiendo del signo que tenga.
Ejemplos:
7x4 = x4 + x4 + x4 + x4 + x4 + x4 + x4 – 3x2 = – x2 – x2 – x2
Exponente numérico: es la cantidad que se encuentra arriba a la derecha de la base, la cual indica la cantidad de veces que la base se toma como producto.
Ejemplos:
5x3 = 5 (x) (x) (x) 8(– x + 5)2 = 8(– x + 5) (– x + 5)
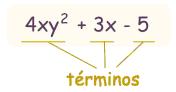
Polinomios
Un polinomio es una suma o resta de monomios (los términos) así:
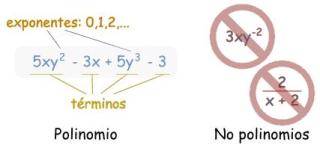
¿Son polinomios o no?
Estos son polinomios:
- 3x
- x – 2
- 3xyz + 3xy2z – 0.1xz – 200y + 0.5
Y estos no son polinomios
- 2/(x+2) no lo es, porque dividir no está permitido
- 3xy-2 no lo es, porque un exponente es «-2» (los exponentes sólo pueden ser 0,1,2,…)
Pero esto sí está permitido:
- x/2 está permitido, porque también es (½)x (la constante es ½, o 0.5)
- también 3x/8 por la misma razón (la constante es 3/8, o 0.375)
OPERACIONES: Sumar polinomios
Dos pasos:
- Pon juntos los términos similares
- Suma los términos similares
Ejemplo: suma 2x2 + 6x + 5 y 3x2 – 2x – 1
Junta los términos similares: 2x2 + 3x2 + 6x – 2x + 5 – 1
Suma los términos similares: (2+3)x2 + (6-2)x + (3-1) = 5x2 + 4x + 4
Sumar en columnas
Puedes sumar varios polinomios juntos así.
Ejemplo: suma (2x2 + 6y + 3xy), (3x2 – 5xy – x) y (6xy + 5)
Ponlos alineados en columnas y suma:
2x2 + 6y + 3xy
3x2 – 5xy – x
6xy + 5
5x2 + 6y + 4xy – x + 5
Usar columnas te ayuda a poner juntos los términos similares en las sumas complicadas.
Restar polinomios
Para restar polinomios, primero invierte el signo de cada término que vas a restar (en otras palabras cambia «+» por «-«, y «-» por «+»), después suma normalmente.
La resta de polinomios consiste en sumar el opuesto del sustraendo.
P(x) − Q(x) = (2x3 + 5x − 3) − (2x3 − 3x2 + 4x)
P(x) − Q(x) = 2x3 + 5x − 3 − 2x3 + 3x2 − 4x
P(x) − Q(x) = 2x3 − 2x3 + 3x2 + 5x− 4x − 3
P(x) − Q(x) = 3x2 + x − 3
Multiplicación de polinomios
Multiplicación de un número por un polinomio
Es otro polinomio que tiene de grado el mismo del polinomio y como coeficientes el producto de los coeficientes del polinomio por el número.
3 · (2x3 − 3 x2 + 4x − 2) = 6x3 − 9x2 + 12x − 6
Multiplicación de un monomio por un polinomio
Se multiplica el monomio por todos y cada uno de los monomios que forman el polinomio.
3 x2 · (2x3 − 3x2 + 4x − 2) = 6x5 − 9x4 + 12x3 − 6x2
Multiplicación de polinomios
P(x) = 2x2 − 3 Q(x) = 2x3 − 3x2 + 4x
Se multiplica cada monomio del primer polinomio por todos los elementos segundo polinomio.
P(x) · Q(x) = (2x2 − 3) · (2x3 − 3x2 + 4x) =
= 4x5 − 6x4 + 8x3 − 6x3 + 9x2 − 12x =
Se suman los monomios del mismo grado.
= 4x5 − 6x4 + 2x3 + 9x2 − 12x
Se obtiene otro polinomio cuyo grado es la suma de los grados de los polinomios que se multiplican.
También podemos multiplicar polinomios de siguiente modo:
División de polinomios
Resolver la división de polinomios: P(x) = x5 + 2x3 − x − 8 Q(x) = x2 − 2x + 1
P(x) : Q(x)
A la izquierda situamos el dividendo. Si el polinomio no es completo dejamos huecos en los lugares que correspondan. A la derecha situamos el divisor dentro de una caja.
Dividimos el primer monomio del dividendo entre el primer monomio del divisor, x5 : x2 = x3 , y multiplicamos cada término del polinomio divisor por el resultado anterior y lo restamos del polinomio dividendo:
Volvemos a dividir el primer monomio del dividendo entre el primer monomio del divisor, 2x4 : x2 = 2 x2 , y el resultado lo multiplicamos por el divisor y lo restamos al dividendo
Procedemos igual que antes: 5x3 : x2 = 5 x
Volvemos a hacer las mismas operaciones, 8x2 : x2 = 8
10x − 6 es el resto, porque su grado es menor que el del divisor y por tanto no se puede continuar dividiendo, y x3+2x2 +5x+8 es el cociente.
División por Ruffini
Si el divisor es un binomio de la forma x — a, entonces utilizamos un método más breve para hacer la división, llamado regla de Ruffini.
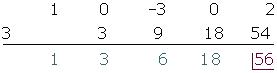
Resolver por la regla de Ruffini la división: (x4 −3x2 +2) : (x −3)
- Si el polinomio no es completo, lo completamos añadiendo los términos que faltan con ceros.
- Colocamos los coeficientes del dividendo en una línea.
- Abajo a la izquierda colocamos el opuesto del término independendiente del divisor.
- Trazamos una raya y bajamos el primer coeficiente.
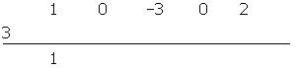
- Multiplicamos ese coeficiente por el divisor y lo colocamos debajo del siguiente término.
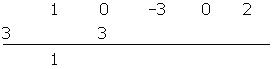
- Sumamos los dos coeficientes.
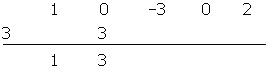
- Repetimos el proceso anterior.
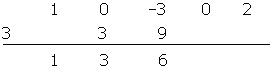
Volvemos a repetir el proceso. Volvemos a repetir.
El último número obtenido, 56 , es el resto.
El cociente es un polinomio de grado inferior en una unidad al dividendo y cuyos coeficientes son los que hemos obtenido: x3 + 3 x2 + 6x +18
Ecuaciones
¿Cuál es el número que falta? ∇ – 2 = 4
Bueno pues, la respuesta es 6, ¿no? Porque 6-2=4.
Bien, en Álgebra no usamos espacios vacíos o cajas sino que usamos una letra (normalmente una x o una y, pero cualquier letra está bien). Entonces escribiríamos: x- 2 = 4
Es así de sencillo. La letra (en este caso una x) sólo quiere decir “aún no lo sabemos” y se la llama frecuentemente incógnita o variable.
Y una vez que la resuelves, escribes: x = 6
Cómo Resolver Ecuaciones:
El álgebra es como un acertijo donde empiezas con algo como “x-2=4” y quieres llegar a algo como “x=6”.
Pero en lugar de decir “obviamente x=6”, usa el siguiente método paso a paso:
- Piensa qué es lo que debes quitar para llegar a “x=…”
- Quítalo haciendo lo opuesto (sumar es opuesto a restar)
- Esto último hazlo en ambos lados
Ecuaciones y fórmulas
¿Qué es una ecuación?: Una ecuación es la IGUALDAD DE DOS EXPRESIONES ALGEBRAICAS. Dicha igualdad se cumple sólo para algunos valores de la incógnita, porque si se cumple para todos es una IDENTIDAD. Por ejemplo: x +2 = 6, es una ecuación dice: hay un número (o varios) tal que si le sumas dos da seis. Evidentemente el número desconocido es el 4.
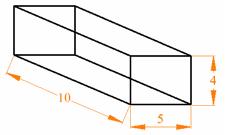 ¿Qué es una fórmula?: Una fórmula es EXPRESIÓN ALGEBRAICA que te permite calcular el valor de una (magnitud) VARIABLE conociendo el valor de otras. Ejemplo: La fórmula para calcular el volumen de una caja es V = lpa
¿Qué es una fórmula?: Una fórmula es EXPRESIÓN ALGEBRAICA que te permite calcular el valor de una (magnitud) VARIABLE conociendo el valor de otras. Ejemplo: La fórmula para calcular el volumen de una caja es V = lpa
V significa volumen, l longitud, p profundidad y a altura.
Si l=5, p=10 y a=4, entonces V = 5×10×4 = 200
Una fórmula tiene más de una variable. Todas estas son ecuaciones, pero sólo algunas son fórmulas:
| x = 2y – 7 | Fórmula (que relaciona x e y) |
| a2 + b2 = c2 | Fórmula (que relaciona a, b y c) |
| x/2 + 7 = 0 | No es una fórmula (sólo una ecuación) |
A veces una fórmula se escribe sin el «=». Ejemplo: la fórmula para el volumen de una caja es: lpa
Pero de alguna manera el «=» está allí, porque podrías haber escrito V = lpa si hubieras querido.
Sujeto de una fórmula. El «sujeto» de una fórmula es la variable sola (normalmente a la izquierda del «=») que es lo que se puede calcular con la expresión algebraica que está a la derecha del “=”.
Ejemplo: en la fórmula s = vt + ½ at2 «s» es el sujeto de la fórmula
Cambiar el sujeto: despejar otra variable. Una de las cosas más poderosas que puede hacer el Álgebra es «transformar» una fórmula para que otra variable sea el sujeto.
Transformar la fórmula del volumen de una caja (V = lpa) para que la longitud sea el sujeto:
| Empieza por: | V = lpa |
| divide los dos lados entre p: | V / p = la |
| divide los dos lados entre a: | V / pa = l |
| intercambia los lados: | l = V / pa |
Así que si tienes una caja con profundidad 2m, altura 2m y volumen 12m3, puedes calcular su longitud: l = V / pa l = 12m3 / (2m×2m) = 12/4 = 3m
En RESUMEN:
Para SABER MÁS:
- Definiciones básicas
- Polinomios
- 3º y 4ºGRADO
- Tercer y Cuarto Grado
- Curso básico de ecuaciones
- ECUACIONES_RUFFINI
- METODO GAUSS SISTEMAS ECUACIONES
- Metodo_gauss_resueltos
ORGANIGRAMA para resolver problemas por métodos algebraicos
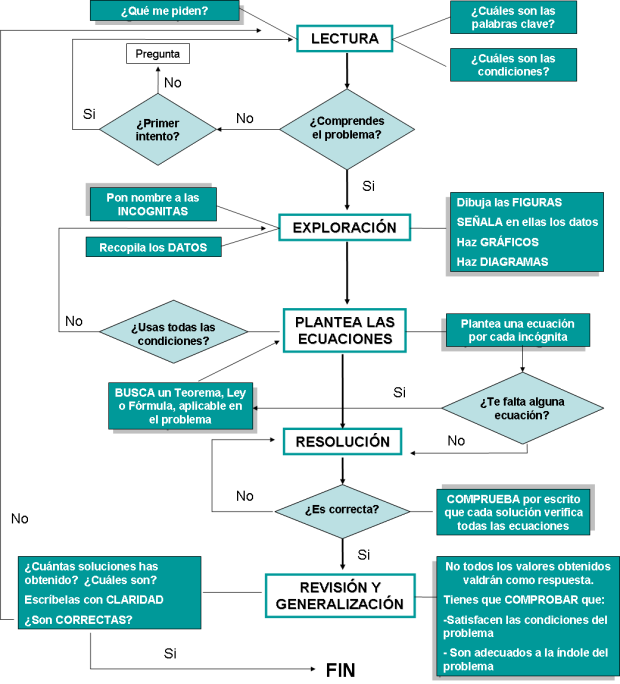
RESOLUCIÓN DE PROBLEMAS POR MÉTODOS ALGEBRAICOS (2ESO) (PDF)
RESOLUCIÓN DE PROBLEMAS POR MÉTODOS ALGEBRAICOS (3ESO) (PDF)
Ejercicios resueltos de ÁLGEBRA: